X-TAL FACTS

The abbreviation X-tal comes from the pronunciation of Crystal.

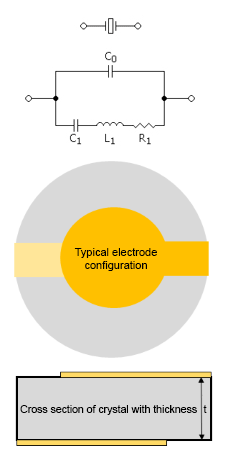
Quartz, chemically crystalline silicon dioxide, SiO₂ is one of many materials that is piezoelectric. It can be modeled as an electromechanical transducer meaning that it will transform mechanical energy to electrical energy. By applying mechanical pressure along certain axes electrical charges will develop along other axes. It is called the direct piezoelectric effect and was discovered 1880 by the brothers Pierre and Jaques Curie. Contrary it will also convert electrical charges to mechanical displacement. It is called the indirect piezoelectric effect and was predicted mathematically by Gabriel Lippmann 1881.In circuit diagrams we assign a symbol (on top of the circuit diagram) to represent the crystal. The crystal can be modeled electrically as a two pole with an equivalent circuit

(under the crystal symbol) in the near vicinity of a mechanical mode. The real equivalent circuit is much more complex because of other unwanted modes but not shown here.

C₀ represents a shunt capacitor which is made up of the two electrodes on opposite sides of the plate used to apply charges on the surfaces to excite a thickness shear vibration. The capacitance is determined by the dielectric constant of quartz and the distance between the electrodes ie the thickness. The frequency of a crystal is inversely proportional to its thickness. For the AT cut the frequency is approximately found to be    where n, denotes operating mode (1,3,5..) and k is constant determined by the velocity of propagation of a thickness  shear wave in the direction along the plate thickness. For an AT cut quartz the constant is approximately 1664 (kHz mm). Example a 0.1 mm thick crystal vibrating on its fundamental mode (n=1) has a frequency of 1664 / 0.1 = 16640 kHz or 16.64 MHz.

Apart from where the crystal has a mechanical resonance the crystal appears as capacitor with the impedance,  If we sweep the frequency near the resonance and study the phase 

response we find two points where the phase passes through zero. The lowest is at the series

resonance frequency,  and the higher is at the anti resonance,

Impedance is minimum at series resonance where the capacitive reactance of C₁ and the inductive reactance of L₁ eliminate each other, leaving only R₁and becomes maximum at anti resonance. A crystal can be excited at its fundamental mode of operation or any odd overtone. Above each main mode so called spurious resonances can occur but is usually not a problem for oscillator applications. Whereas in filter applications they can be detrimental for the result.In order to excite the mechanical vibrations we need to apply charges on the surfaces which we do by connecting the crystal to an electric circuit called oscillator.

In the oscillator we can tune the excitation frequency by various means so that it 
corresponds to the mechanical frequency of the quartz crystal so that the oscillation conditions can be met and sustained. The major reason for the success of using quartz crystal is the high Q value obtained in combination with the low temperature dependence. The Q-value which can be written

  or  is called the unloaded Q. When the crystal is inserted into an oscillator

the Q-value will be loaded hence lower. The close in Phase Noise in the oscillator is directly proportional to the loaded Q-value. Also the motional capacitance influence the Phase Noise. The lower the better. If low Phase Noise is the objective the use of overtone in oscillators is preferred. However when C1 diminishes the tuning range reduces correspondingly. Therefore fundamental use is best for large tuning applications.Another way to improve the Phase Noise is to use the SC cut. There are other advantages using SC cut crystals. Improved transient response for temperature changes. A smaller amplitude – frequency effect is apparent enabling higher crystal current leading to a better S/N ratio hence lower Phase Noise floor. The back side is higher production cost and necessity to add a trap in the oscillator for the b-mode which is about 10 % higher in frequency. Coupling to other modes are also less prevalent for SC cuts.